UNIDAD 2: Matrices y Determinantes
Definición de Matriz
Las Matrices son arreglos rectangulares de números encerrados entre paréntesis o corchetes. Las denotamos con letras mayúsculas: A, B, C,... y a sus elementos les llamamos componentes o entradas y se representan con letras minúsculas: a, b, c,... o también con ai j, en donde el subíndice i indica el renglón (fila) en donde se encuentra el componente y el subíndice j nos indica en qué columna está.
Ejemplo:
 mxn
mxn
a) Suma y Resta

Observa que para sumar y restar debes sumar y restar las entradas correspondientes de las dos matrices.
Ejemplo 2)

Responde a)¿De qué orden son las matrices del ejemplo 1 y 2 y sus respectivas matrices que son suma o resta?
b) En el ejemplo 2 ¿Cuál es el elemento a22, a13, b13, b21?
b) Producto de un escalar por una matriz


Tarea: Verifica las propiedades de la mutiplicación por un escalar utizando para ello una matriz de orden 3x4 y escalares c, d.
SelSea a
Las Matrices son arreglos rectangulares de números encerrados entre paréntesis o corchetes. Las denotamos con letras mayúsculas: A, B, C,... y a sus elementos les llamamos componentes o entradas y se representan con letras minúsculas: a, b, c,... o también con ai j, en donde el subíndice i indica el renglón (fila) en donde se encuentra el componente y el subíndice j nos indica en qué columna está.
Ejemplo:
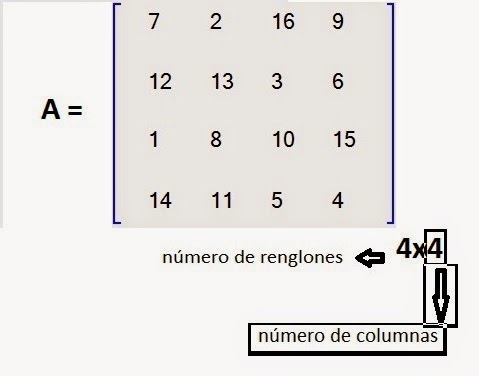
En este caso decimos que la Matriz A es de Orden 4 x 4
Elemento en el tercer renglón y en la segunda columna: a32 = 8,
Elemento en el primer renglón y en la tercera columna: a13 = 16,
Elemento en el cuarto renglón y en la cuarta columna: a44 = 4,...
En general tenemos:
orden
Operaciones con Matrices:
Para estar bien definidas la suma y la resta de matrices deben ser del mismo orden; es decir deben tener el mismo número de renglones y de columnas.
Ejemplo 1)
Observa que para sumar y restar debes sumar y restar las entradas correspondientes de las dos matrices.
Ejemplo 2)
Responde a)¿De qué orden son las matrices del ejemplo 1 y 2 y sus respectivas matrices que son suma o resta?
b) En el ejemplo 2 ¿Cuál es el elemento a22, a13, b13, b21?
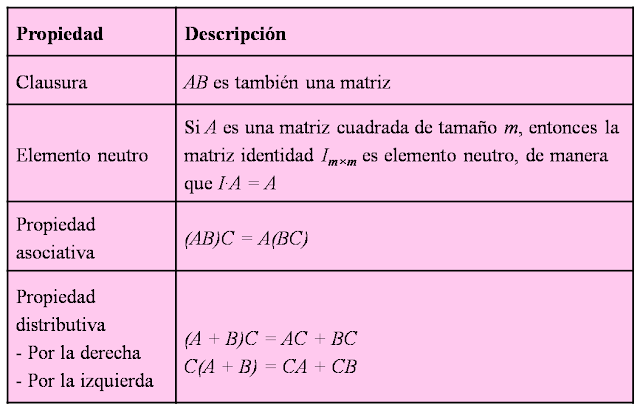
Propiedades de la suma de Matrices
Sean A, B y C cualesquiera matrices del mismo orden mxn entonces
- Asociativa: (A+B)+C = A + (B+C)
- Conmutativa: A + B= B + A
- Elemento neutro: A + O = A ; O es la Matriz cuyas entradas son todas cero
- Elemento inverso: A + ( -A ) = A - A = O
b) Producto de un escalar por una matriz
Propiedades de la multiplicacón por escalar
Tarea: Verifica las propiedades de la mutiplicación por un escalar utizando para ello una matriz de orden 3x4 y escalares c, d.
c) Multiplicación de matrices

- Sean A y B dos matrices.
- Para poder realizar la multiplicación de ellas debemos de verificar que en la primera matriz sea el números de columnas igual al número de renglones de la segunda matriz.
- El orden de la matriz multiplicación es el número de renglones de la primera matriz por el número de columnas de la segunda matriz.
Es decir, si A4x2, B2x3
entonces (AB)4x3
Ejemplo: Sean A3x3 y B3x2 las matrices dadas a continuación:
Para obtener la matriz multiplicación C se calculan los elementos cij los cuales se calculan de forma que:
c11 = 6(4)+(-8)(5)+(-2)(3) = -22 (primer renglón de A por primera columna de B)
c12 = 6(3)+(-8)(-7)+(-2)(5) = 64 (primer renglón de A por segunda columna de B)
c21 = 1(4)+0(5)+2(3) = 10 (segundo renglón de A por primera columna de B)
- i el renglón que tomaremos de la primer matriz (A)
- j la columna de la segunda matriz (B).
c11 = 6(4)+(-8)(5)+(-2)(3) = -22 (primer renglón de A por primera columna de B)
c12 = 6(3)+(-8)(-7)+(-2)(5) = 64 (primer renglón de A por segunda columna de B)
c21 = 1(4)+0(5)+2(3) = 10 (segundo renglón de A por primera columna de B)
c22 = 1(3)+0(-7)+2(5) = 13 (segundo renglón de A por segunda columna de B)
c31 = -1(4)+2(5)+ (-5)(3) = -9 (tercer renglón de A por primera columna de B)
c32 = -1(3)+2(-7)+ (-5)(5) = -42 (tercer renglón de A porsegunda columna de B)
Como se ve, la nueva matriz C3x2 que se genera de la multiplicación de A y B la podemos realizar más fácilmente ayudándonos de sus elementos ci j,

Ejercicio :
1. Indica (en el ejemplo anterior) si son posibles de realizar:
a) A+B,
b) B-A,
c) BA,
d) -3A,
e) (1/4) B
2. Si lo son efectúa las operaciones y escribe el resultado, en caso contrario explica qué falló.
3. Haz a las matrices A y B escalonadas.
Como se ve, la nueva matriz C3x2 que se genera de la multiplicación de A y B la podemos realizar más fácilmente ayudándonos de sus elementos ci j,
Propiedades de la multiplicación de Matrices
Sean A, B y C cualesquiera matrices tales que esté bien definida su suma o su multiplicación entre ellas entonces

Ejercicio :
1. Indica (en el ejemplo anterior) si son posibles de realizar:
a) A+B,
b) B-A,
c) BA,
d) -3A,
e) (1/4) B
2. Si lo son efectúa las operaciones y escribe el resultado, en caso contrario explica qué falló.
3. Haz a las matrices A y B escalonadas.