Temario

-
    1 Números complejos C.

    1. Definición, origen y operaciones (suma,resta,multiplicación y división) de los números complejos 
    2. Potencias de “i”, 
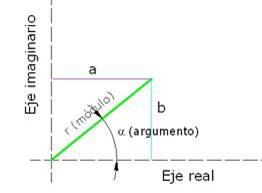
    3. Argumento, módulo o valor absoluto.
    4. Forma polar y exponencial.
    5. Teorema de De Möivre, potencias y extracción de raíces. Ecuaciones polinómicas


    2 Matrices y determinantes

    1. Matrices
    a.       Definición, notación, orden y operaciones
     básicas.
    b.      Propiedades y Clasificación
    c.       Escalonamiento, rango e inversa.
    1. Determinantes de nxn.
    a.       Definición y  propiedades
    b.      Inversa de una matriz cuadrada a través de la adjunta.
    c.       Aplicación


     3 Sistemas de Ecuaciones Lineales (SEL).

    1. Definición, Clasificación de SEL.
    2. Tipos de solución e Interpretación geométrica.
    3. Métodos de solución de un SEL: Gauss, Gauss-Jordan, regla de Cramer e Inversa de una matriz


     4 Espacios vectoriales.

    1. Definición
    2. Subespacio Vectorial y Propiedades.
    3. Bases y Dimensión.
    4. Cambio de base
    5. Producto interno y propiedades.
    6. Base ortonormal.
       

     5 Transformaciones lineales.

    1. Introducción a las transformaciones lineales.
    2. Núcleo e imagen.
    3. La matriz de una transformación lineal.
    4. Aplicación de las transformaciones lineales: reflexión, dilatación, rotación  y contracción.
        


Fuentes de información



1.Strang, Gilbert. áLgebra LineaL 
y sus apLicaciones. Thomson, 2007.

 
 2.Hitt, Fernando, Álgebra Lineal. Prentice Hall, 2002
     3.Hill, Richard. Álgebra Lineal Elemental con Aplicaciones. Prentice Hall, 1997
     4.Anton, Howard. Introducción al álgebra lineal. Limusa 2008.
     5.Grossman, Stanley I. Algebra lineal. McGraw-Hill, 2008.



Comentarios

Publicar un comentario

Entradas más populares de este blog

UNIDAD 3: SISTEMAS DE ECUACIONES LINEALES (SEL)

-
Imagen
Un sistema de ecuaciones lineales puede ser de dos ecuaciones lineales con dos incógnitas (variables) 2x2:                a 1 1 x 1 +  a 1 2   x 2  =  b 1                  a 2 1 x 1 +  a 2 2   x 2  =  b 2 ; donde   a i j y   b i son números reales  i = j = 1,2  y   a i j  distinto de cero en al menos una de las ecuaciones.  tres ecuaciones lineales con tres incógnitas (variables) de 3x3:               a 1 1 x 1 +  a 1 2   x 2 + a 1 3 x 3 =  b 1               a 2 1 x 1 +  a 2 2   x 2 + a 2 3 x 3 =  b 2               a 3 1 x 1 +  a 3 2   x 2 + a 3 3 x 3 =  b 3 ; donde   a i j  y   b i  son números reales     i = j = 1,2,3   y    a i j   distinto de cero  en al menos una de las ecuaciones.  En general: n ecuaciones lineales con n incógnitas (variables) de nxn:                   a 1 1  x 1 + a 1 2 x 2 + . . . +  a 1 n  x n = b 1                   a 2 1  x 1 +  a 2 2   x 2 + . . . +  a 2 n  x n =  b 2                                             
Leer más

UNIDAD 2: Matrices y Determinantes

-
Imagen
Definición de Matriz Las  Matrices   son arreglos rectangulares de números encerrados entre paréntesis o corchetes. Las denotamos con letras mayúsculas: A, B, C ,... y a sus elementos les llamamos componentes o entradas y se representan con letras minúsculas:  a, b, c ,... o también con a i j, en donde el subíndice i indica el renglón (fila) en donde se encuentra el componente y el subíndice j nos indica en qué columna está. Ejemplo:                            En este caso decimos que la Matriz A es de Orden  4 x 4                                                     Elemento en el tercer renglón y en la segunda columna:  a 32 = 8,  Elemento en el primer renglón y en la tercera columna:  a 13  = 16,  Elemento en el cuarto renglón y en la cuarta columna:  a 44  = 4,... En general tenemos:                              mxn                                                 orden     Operaciones con Matrices: a) Suma y Resta Para estar bien defini
Leer más

Tema 3: Método de Gauss-Jordan, Gauss, Regla de Cramer y la Matriz Inversa.

-
Imagen
Matriz Inversa por el método de Gauss-Jordan A continuación la resolución de sistemas de ecuaciones lineales Método de Gauss-Jordan y Gauss s. https://cursoscienciasbasicas.blogspot.com/2020/04/solucion-de-un-sel-por-el-metodo-de.html Fuente: http:// www.krellinst.org/AiS/textbook/unit2/example_projects/starter/math/matrix/gauss.html Método de GAUSS Método de gauss   from  pepemunoz Método de la Regla de Cramer Regla de cramer o método por determinantes   from  Matematica de Samos Método de la Inversa Sea el siguiente sistema se ecuaciones lineales de nxn: Podemos representar el sistema anterior de la forma matricial  -->  A X = B; en donde La matriz A se llama matriz del sistema, es de dimensión n x n y sus elementos son los coeficientes de las incógnitas. La matriz X es una matriz columna, de dimensión n x 1, formada por las incógnitas del sistema. Por último, la matriz B es otra matriz columna, de dimensión n x 1, for
Leer más