Tema 1: Raíces n-ésimas de un número complejo dado.
TEMA 1: Ejercicios de operaciones con números complejos.
Ejercicios de Números complejos
Entradas más populares de este blog
Tema 1: Representación de los números Complejos y sus operaciones: Suma, Resta, Multiplicación y División
Definición y notación de los números complejos, operaciones entre complejos <--Darle clic Operaciones con números complejos : Notaciones de los números complejos: z = a + b i = (a, b) Ejemplos. Dados Z 1=(3,−2) , Z 2=(1,5), hallar: a) Z 1+ Z 2, b) Z 1 Z 2. a) Z 1+ Z 2=( 3 ,-2)+( 1 ,5)=( 3 + 1 ,-2+5)=( 4 ,3)= 4 +3 i b) Z 1 Z 2=( 3 ,-2)( 1 ,5) = [ 3 ( 1 ) - (-2)(5), 3 (5) + (-2)( 1 )] =(3+10,15-2)=(13,13)=13+13 i c)Dados (1, 3/2) , (2,1), hallar: ( 1 ,3/2)+( 2 ,1). ( 1 ,3/2)+( 2 ,1)=( 1 + 2 ,3/2+1)=( 3 ,5/2)= 3 +(5 /2) i En la notación binómica: a+bi, tendremos el siguiente desarrollo a) Z 1+ Z 2 =(3-2i)+(1+5i)= 3+1+(-2i+5i)=4+3i b) Z 1 Z 2 =( 3 -2i)( 1 + 5i) = 3 ( 1 )+ 3 (5i)+ (-2i)( 1 )+ (-2i)(5i) = 3+15i-2i-10 i ^ 2 =3 -13i +10; pues i^2 =-1 ...
Temario
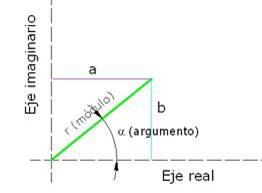
1 Números complejos C . Definición, origen y operaciones (suma,resta,multiplicación y división) de los números complejos Potencias de “ i ”, Argumento, módulo o valor absoluto. Forma polar y exponencial. Teorema de De Möivre, potencias y extracción de raíces. Ecuaciones polinómicas 2 Matrices y determinantes Matrices a. Definición, notación, orden y operaciones básicas. b. Propiedades y Clasificación c. Escalonamiento, rango e inversa. Determinantes de nxn. a. Definición y propiedades b. Inversa de una matriz cuadrada a través de la adjunta. c. Aplicación 3 Sistemas de Ecuaciones Lineales (SEL). Definición, Clasificación de SEL. Tipos de solución e Interpret...