Tema 1: Representación de los números Complejos y sus operaciones: Suma, Resta, Multiplicación y División

-


Definición y notación de los números complejos,  operaciones entre complejos <--Darle clic

Operaciones con números complejos :


  Notaciones de los números complejos: z = a + b i = (a, b)

Ejemplos.
 Dados Z1=(3,−2) , Z2=(1,5),  hallar: a) Z1+Z2, b) Z1Z2.

a) Z1+Z2=(3,-2)+(1,5)=(3+1,-2+5)=(4,3)=4+3i

b) Z1Z2=(3,-2)(1,5) = [3(1)-(-2)(5), 3(5)+(-2)(1)] =(3+10,15-2)=(13,13)=13+13i

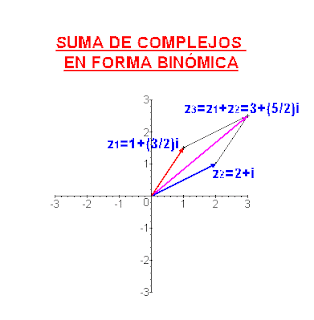
c)Dados (1,3/2) , (2,1),  hallar:(1,3/2)+(2,1).

 (1,3/2)+(2,1)=(1+2,3/2+1)=(3,5/2)=3+(5/2)i

 En la notación binómica: a+bi, tendremos el  siguiente desarrollo

a)Z1+Z2=(3-2i)+(1+5i)= 3+1+(-2i+5i)=4+3i

 b)Z1Z2=(3-2i)(1+5i) = 3(1)+3(5i)+(-2i)(1)+(-2i)(5i)
                =3+15i-2i-10i^2 =3 -13i +10; pues i^2 =-1
                        =13-13i

 Ejercicios 
1. Después de ver el documento del enlace (Definición y notación de los números complejos,  operaciones entre complejos https://www.blogger.com/blog/post/edit/1873456732613776406/6770289875529522830# ),
 contesta las pregunta siguientes:
I. ¿Cuáles números son complejos y cómo se representan geométricamente?
II. ¿Qué notación usamos para representarlos?
III. ¿Cómo se define el opuesto y el conjugado de un número complejo?
IV. ¿Qué nombre reciben en el plano complejo el eje horizontal y el eje vertical?

2. Si  Z1=(1,3/2) , Z2=(2,1), encuentra usando la notación binómica: a+bi 
      I. la suma: Z1+Z2  y
       II. la multiplicación: Z1Z2, 
 en el desarrollo de las operaciones.


Entradas más populares de este blog

UNIDAD 3: SISTEMAS DE ECUACIONES LINEALES (SEL)

-
Imagen
Un sistema de ecuaciones lineales puede ser de dos ecuaciones lineales con dos incógnitas (variables) 2x2:                a 1 1 x 1 +  a 1 2   x 2  =  b 1                  a 2 1 x 1 +  a 2 2   x 2  =  b 2 ; donde   a i j y   b i son números reales  i = j = 1,2  y   a i j  distinto de cero en al menos una de las ecuaciones.  tres ecuaciones lineales con tres incógnitas (variables) de 3x3:               a 1 1 x 1 +  a 1 2   x 2 + a 1 3 x 3 =  b 1               a 2 1 x 1 +  a 2 2   x 2 + a 2 3 x 3 =  b 2               a 3 1 x 1 +  a 3 2   x 2 + a 3 3 x 3 =  b 3 ; donde   a i j  y   b i  son números reales     i = j = 1,2,3   y    a i j   distinto de cero  en al menos una de las ecuaciones.  En general: n ecuaciones lineales con n incógnitas (variables) de nxn:                   a 1 1  x 1 + a 1 2 x 2 + . . . +  a 1 n  x n = b 1                   a 2 1  x 1 +  a 2 2   x 2 + . . . +  a 2 n  x n =  b 2                                             
Leer más

Tema 3: Método de Gauss-Jordan, Gauss, Regla de Cramer y la Matriz Inversa.

-
Imagen
Matriz Inversa por el método de Gauss-Jordan A continuación la resolución de sistemas de ecuaciones lineales Método de Gauss-Jordan y Gauss s. https://cursoscienciasbasicas.blogspot.com/2020/04/solucion-de-un-sel-por-el-metodo-de.html Fuente: http:// www.krellinst.org/AiS/textbook/unit2/example_projects/starter/math/matrix/gauss.html Método de GAUSS Método de gauss   from  pepemunoz Método de la Regla de Cramer Regla de cramer o método por determinantes   from  Matematica de Samos Método de la Inversa Sea el siguiente sistema se ecuaciones lineales de nxn: Podemos representar el sistema anterior de la forma matricial  -->  A X = B; en donde La matriz A se llama matriz del sistema, es de dimensión n x n y sus elementos son los coeficientes de las incógnitas. La matriz X es una matriz columna, de dimensión n x 1, formada por las incógnitas del sistema. Por último, la matriz B es otra matriz columna, de dimensión n x 1, for
Leer más

UNIDAD 2: Matrices y Determinantes

-
Imagen
Definición de Matriz Las  Matrices   son arreglos rectangulares de números encerrados entre paréntesis o corchetes. Las denotamos con letras mayúsculas: A, B, C ,... y a sus elementos les llamamos componentes o entradas y se representan con letras minúsculas:  a, b, c ,... o también con a i j, en donde el subíndice i indica el renglón (fila) en donde se encuentra el componente y el subíndice j nos indica en qué columna está. Ejemplo:                            En este caso decimos que la Matriz A es de Orden  4 x 4                                                     Elemento en el tercer renglón y en la segunda columna:  a 32 = 8,  Elemento en el primer renglón y en la tercera columna:  a 13  = 16,  Elemento en el cuarto renglón y en la cuarta columna:  a 44  = 4,... En general tenemos:                              mxn                                                 orden     Operaciones con Matrices: a) Suma y Resta Para estar bien defini
Leer más