Tema 1: Forma Polar de un Número Complejo

-

TEMA 1: Números Complejos

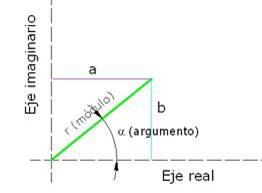
 La forma Polar de un número complejo z = a+bi = (a,b)

Para encontrar la forma polar del complejo z usamos el triángulo rectángulo que podemos formar con las coordenadas (a, b). Por el Teorema de Pitágoras y definición de la función trigonométrica 

tan (𝛳) = cateto opuesto / cateto adyacente obtenemos:

Matemática Avanzada - EPN: Octubre


Por lo Tanto la forma polar de z=a+bi es:  Si r = | z |= , arg(z) = 𝛳=tan⁻¹(b/a), entonces z = r [cos𝛳+i sen𝛳 ]=rθ.

La forma trigonométrica es por la definición de las funciones cos 𝛳 y sen 𝛳 en el triángulo rectángulo:

 cos 𝛳 = a/r =cateto adyacente/hipotenusa, por lo que: a = r cos 𝛳

sen 𝛳 = b/r =cateto opuesto/hipotenusa, por lo que: b = r sen 𝛳

Nota1:El sentido del ángulo 𝛳 es positivo, cuando gira a partir del eje real positivo, contrario a las manecillas del reloj.

Nota2: Respecto al ángulo 𝛳, siempre que la parte real del número complejo z es negativa, tenemos que rectificar el ángulo 𝛳 sumando 180°  

Ejemplos:

Encontrar las coordenadas polares de los siguientes números complejos 

a) z₁ = 3 - i

  b) z₂ = 1/2+3i

 c) z₃ = (-1, -1/5)






Comentarios

Publicar un comentario

Entradas más populares de este blog

UNIDAD 3: SISTEMAS DE ECUACIONES LINEALES (SEL)

-
Imagen
Un sistema de ecuaciones lineales puede ser de dos ecuaciones lineales con dos incógnitas (variables) 2x2:                a 1 1 x 1 +  a 1 2   x 2  =  b 1                  a 2 1 x 1 +  a 2 2   x 2  =  b 2 ; donde   a i j y   b i son números reales  i = j = 1,2  y   a i j  distinto de cero en al menos una de las ecuaciones.  tres ecuaciones lineales con tres incógnitas (variables) de 3x3:               a 1 1 x 1 +  a 1 2   x 2 + a 1 3 x 3 =  b 1               a 2 1 x 1 +  a 2 2   x 2 + a 2 3 x 3 =  b 2               a 3 1 x 1 +  a 3 2   x 2 + a 3 3 x 3 =  b 3 ; donde   a i j  y   b i  son números reales     i = j = 1,2,3   y    a i j   distinto de cero  en al menos una de las ecuaciones.  En general: n ecuaciones lineales con n incógnitas (variables) de nxn:                   a 1 1  x 1 + a 1 2 x 2 + . . . +  a 1 n  x n = b 1                   a 2 1  x 1 +  a 2 2   x 2 + . . . +  a 2 n  x n =  b 2                                             
Leer más

UNIDAD 2: Matrices y Determinantes

-
Imagen
Definición de Matriz Las  Matrices   son arreglos rectangulares de números encerrados entre paréntesis o corchetes. Las denotamos con letras mayúsculas: A, B, C ,... y a sus elementos les llamamos componentes o entradas y se representan con letras minúsculas:  a, b, c ,... o también con a i j, en donde el subíndice i indica el renglón (fila) en donde se encuentra el componente y el subíndice j nos indica en qué columna está. Ejemplo:                            En este caso decimos que la Matriz A es de Orden  4 x 4                                                     Elemento en el tercer renglón y en la segunda columna:  a 32 = 8,  Elemento en el primer renglón y en la tercera columna:  a 13  = 16,  Elemento en el cuarto renglón y en la cuarta columna:  a 44  = 4,... En general tenemos:                              mxn                                                 orden     Operaciones con Matrices: a) Suma y Resta Para estar bien defini
Leer más

Tema 3: Método de Gauss-Jordan, Gauss, Regla de Cramer y la Matriz Inversa.

-
Imagen
Matriz Inversa por el método de Gauss-Jordan A continuación la resolución de sistemas de ecuaciones lineales Método de Gauss-Jordan y Gauss s. https://cursoscienciasbasicas.blogspot.com/2020/04/solucion-de-un-sel-por-el-metodo-de.html Fuente: http:// www.krellinst.org/AiS/textbook/unit2/example_projects/starter/math/matrix/gauss.html Método de GAUSS Método de gauss   from  pepemunoz Método de la Regla de Cramer Regla de cramer o método por determinantes   from  Matematica de Samos Método de la Inversa Sea el siguiente sistema se ecuaciones lineales de nxn: Podemos representar el sistema anterior de la forma matricial  -->  A X = B; en donde La matriz A se llama matriz del sistema, es de dimensión n x n y sus elementos son los coeficientes de las incógnitas. La matriz X es una matriz columna, de dimensión n x 1, formada por las incógnitas del sistema. Por último, la matriz B es otra matriz columna, de dimensión n x 1, for
Leer más