Temario
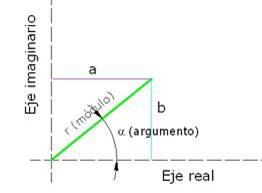
1 Números complejos C . Definición, origen y operaciones (suma,resta,multiplicación y división) de los números complejos Potencias de “ i ”, Argumento, módulo o valor absoluto. Forma polar y exponencial. Teorema de De Möivre, potencias y extracción de raíces. Ecuaciones polinómicas 2 Matrices y determinantes Matrices a. Definición, notación, orden y operaciones básicas. b. Propiedades y Clasificación c. Escalonamiento, rango e inversa. Determinantes de nxn. a. Definición y propiedades b. Inversa de una matriz cuadrada a través de la adjunta. c. Aplicación 3 Sistemas de Ecuaciones Lineales (SEL). Definición, Clasificación de SEL. Tipos de solución e Interpret...